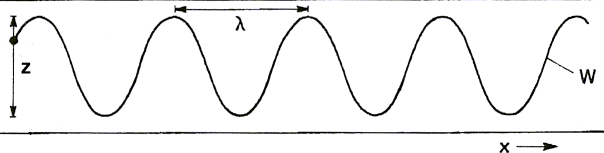
| z: Vibrierender Taststift mit der Amplitude �A0 λ: Wellenl�nge x: Bandgeschwindigkeit c w: Resultierende Welle Abbildung 1a: Vibrierender Taststift auf einem vorbeilaufenden Papierband |
![[Photo of the author]](../../common/images/John-Perr.gif)
original in fr John Perr
fr to en John Perr
en to de Josef Schwarz
Linux-Anwender seit 1994; einer der franz�sischen Autoren von LinuxFocus; Maschinenbauingenieur, MSc Sound and Vibration Studies
Dieser Artikel bietet Grundlegendes zu Akustik und Signalverarbeitung
f�r Musiker und Informatiker..
Wer je davon getr�umt hat, seine eigenen Musikaufnahmen zu machen,
oder am Computer mit Musik herumzuspielen, sollte weiterlesen.
![[Illustration]](../../common/images/article271/illustration271.png)
Dieser Artikel soll dem Leser ein Grundwissen �ber Schall (Sound) und Schallverarbeitung geben.
Nat�rlich wird ein Hauptaugenmerk auf Musik liegen, aber alles in allem ist Musik doch nur
Schall wie jedes andere Ger�usch auch, nur eben angenehmer zu h�ren.
Zuerst werden die physikalischen Konzepte von Schall pr�sentiert, und die Art und Weise,
wie das menschliche Ohr ihn interpretiert. Dann werden Signale betrachtet, z.B. wie sich Schall
ver�ndert, wenn er aufgenommen wird, besonders mit modernen digitalen Ger�ten wie Sampler oder Computer.
Zuletzt wird auf aktuelle Kompressionstechnologien wie mp3 oder Ogg vorbis eingegangen.
Die Themen, die in diesem Artikel zur Sprache kommen, sollten einem breiten Publikum verst�ndlich
sein. Der Autor versucht sein Bestes, eine "normale Sprache" zu verwenden und besonders Ausdr�cke, die
Musikern vertraut sind. Ein paar wenige mathematische Formeln tauchen hie und da in den Abbildungen auf,
sind hier aber nicht weiter wichtig (puuh! Gott sei Dank...).
Physikalisch gesprochen ist Schall mechanisches Vibrieren von gasf�rmigen, fl�ssigen oder festen
Medien. Die Elastizit�t des Mediums erlaubt dem Schall, sich von der Schallquelle weg als Wellen
auszubreiten, genauso wie die Kreise, die von einem ins Wasser geworfenen Stein ausgehen.
Jedes Mal, wenn ein Objekt vibriert, geht ein kleiner Anteil seiner Energie an die Umgebung
als Schall verloren. Um es gleich zu sagen, Schall kann sich nicht in Vakuum ausbreiten.
Abbildung 1a zeigt, wie ein Taststift, der mit einer vibrierenden Quelle, z.B. einem Lautsprecher,
verbunden ist, eine Wellenlinie zeichnet, wenn darunter ein Papierband vorbeil�uft.

| z: Vibrierender Taststift mit der Amplitude �A0 λ: Wellenl�nge x: Bandgeschwindigkeit c w: Resultierende Welle Abbildung 1a: Vibrierender Taststift auf einem vorbeilaufenden Papierband |
In der Luft pflanzen sich Schallwellen als �nderungen des Luftdrucks fort. Ein Lautprecher
verursacht Luftdruck�nderungen in der umgebenden Luft. Diese (schwachen) �nderungen des Drucks
setzen sich durch die Luft fort. Wichtig ist, dass sich nur der Druck fortpflanzt,
nicht aber die Luft selber. Auch beim Beispiel mit den sich ausbreitenden Kreisen im Wasser,
das ich zuvor angesprochen habe, pflanzen sich nur die Wellen fort, das Wasser bleibt aber
am selben Platz. Ein schwimmendes Objekt bewegt sich nur auf und ab. Das ist auch
der Grund daf�r, dass man vor einem Lautsprecher keinen "Wind" versp�rt. Schallwellen
pflanzen sich mit etwa 344 Metern pro Sekunde fort, in Luft bei 20�C, aber die
Luftteilchen selbst bewegen sich nur ein paar Mikrometer vor und zur�ck.

Wir wissen inzwischen aus den obigen Abbildungen, dass Schallwellen eine sinusf�rmige Form haben.
Der Abstand zwischen zwei Scheitelpunkten wird Wellenl�nge genannt und die Anzahl der
Scheitelpunkte, die ein Beobachter in einer Sekunde sieht, ist die Frequenz. Dieser in der
Physik verwendete Begriff ist f�r einen Musiker nichts anderes als die Tonh�he. Niedrige Frequenzen
ergeben Basst�ne, w�hrenddessen hohe Frequenzen hohe T�ne ergeben.
Abbildung 2
zeigt sowohl Frequenz als auch Wellenl�nge von Schallwellen, die sich in Luft ausbreiten:

Ein anderes Merkmal von Schall ist seine Amplitude. Schall kann leise oder laut sein. Das entspricht kleinen oder gro�en Schwankungen des Luftdrucks, je nach der Kraft, mit der die Luft zusammengedr�ckt wird. Um die St�rke von Schall (Schalldruck) zu bewerten, wird die Einheit Dezibel (dB) verwendet. Dezibel scheint eine eher schwierige Einheit zu sein, wie Abbildungen 3a und 3b zeigen. Es wurde gew�hlt, weil sich damit nichtsdestotrotz einfach rechnen l�sst, und weil der Logarithmus dem menschlichen H�rverhalten entspricht, wie wir im n�chsten Kapitel sehen werden. Ganz ohne Zweifel verwenden wir beim H�ren Mathematik, ohne es zu merken:
| Abbildung 3a: Schalldruck | Abbildung 3b: Leistungspegel |
Bis jetzt m�ssen wir nur wissen, dass dB sich auf den Leistungspegel
beziehen. 0 dB entsprechen der unteren menschlichen H�rschwelle und sagen nicht aus, dass
kein Schall vorhanden w�re. Dezibel ist eine Ma�einheit f�r Schall, die den
menschlichen Wahrnehmungsgrenzen entspricht. �nderungen des Bezugspunktes (Po
oder Wo) �ndern dementsprechend den dB-Wert. Darum entspricht die dB-Angabe
am Lautst�rkeregler des HiFi-Verst�rkers nicht dem Ger�uschpegel, sondern der
elektrischen Ausgangsleistung des Verst�rkers.
Das ist also eine komplett andere Ma�einheit, da 0 dB oft die maximale
Ausgangsleistung des Verst�rkers bezeichnet. Akustisch betrachtet ist die
Lautst�rke viel gr��er, sonst h�ttest du dir wohl nicht diesen besonderen
Verst�rker gekauft, aber es h�ngt auch von der Effizienz der Lautsprecher ab...
Abbildung 4 zeigt uns Amplitude und Frequenz verschiedener, bekannte Schallquellen.
Die geschwungenen Linien verbinden, was das menschliche Geh�r als gleich laut
empfindet; darauf werden wir sp�ter noch genauer eingehen:

Die nachstehende Tabelle zeigt Pegel verbreiteter Schallquellen in Dezibel und Watt. Achte darauf, wie die Verwendung von Dezibel als Einheit die Notation vereinfacht.
| Leistung (Watt) | Pegel dB | Beispiel | Leistung (W) |
|---|---|---|---|
| 100 000 000 | 200 | Saturn V Rakete 4 Duesenflugzeuge |
50 000 000 50 000 |
| 1 000 000 | 180 | ||
| 10 000 | 160 | ||
| 100 | 140 | Gro�es Orchester | 10 |
| 1 | 120 | Mei�elhammer | 1 |
| 0.01 | 100 | Sprache: Schreien | 0.001 |
| 0.000 1 | 80 | ||
| 0.000 001 | 60 | Sprache: Unterhaltung | 20x10-6 |
| 0.000 000 01 | 40 | ||
| 0.000 000 000 1 | 20 | Sprache: Fl�stern | 10-9 |
| 0.000 000 000 001 | 0 | ||
| Schalldruck einiger typischer Schallquellen | |||
Die Schallamplitude kann auf verschiedene Weise gemessen werden. Das gilt auch f�r andere Wellensignale wie Abbildung 5 zeigt:

| Symbol | Name | Definition |
|---|---|---|
| ADurchschnitt | durchschnittliche Amplitude | arithmet. Mittel des positiven Signalteils |
| ARMS | quadrat. Mittelwert | Amplitude proportional zum Energieinhalt |
| AScheitelwert | h�chste Amplitude | maximale positive Amplitude |
| Adoppelter Scheitelwert | Amplitude des doppelten Scheitelwerts | maximale positive bis negative Amplitude |
Die durchnittliche Amplitude ist nur eine theoretische Ma�zahl, die technisch nicht verwendet wird. Der quadratische Mittelwert wird hingegen allgemein verwendet, um �quivalente Signale und im Besonderen Sinuswellen zu messen. Zum Beispiel ist die Spannung, die bei uns mit 220 Volt aus der Steckdose kommt, eigentlich eine Sinuswelle mit einer Frequenz von 50 Hertz (Hz). Dabei sind die 220 Volt der quadratische Mittelwert, so dass der Wert eigentlich zwischen -311 Volt und -311 Volt schwingt. Wenn wir die andere Definition verwenden, dann hat das Signal einen Scheitelwert von 311 Volt oder 622 Volt doppelten Scheitelwert. Dieselben Definitionen werden f�r das Ausgangssignal des Verst�rkers verwendet, das zu den Lautsprechern f�hrt. Ein Verst�rker, der 10 Watt in quadrat. Mittelwert liefert, erreicht damit einen Scheitelwert von 14 Watt und einen doppelten Scheitelwert von 28 Watt. Im Handel wird f�r die Leistung eines Verst�rkers gerne der doppelte Scheitelwert propagiert, weil er nat�rlich h�her ist und imposanter klingt.
Zeit spielt eine gewichtige Rolle in der Akustik.
Zeit und Raum sind sehr eng miteinander verkn�pft, da Schall
eine Welle ist, die sich �ber die Zeit im Raum fortpflanzt.
Wenn man das bedenkt, kann man drei Arten von akustischen
Signalen definieren:
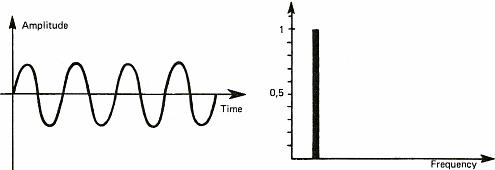
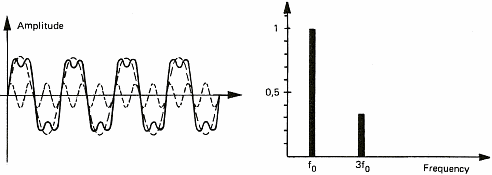
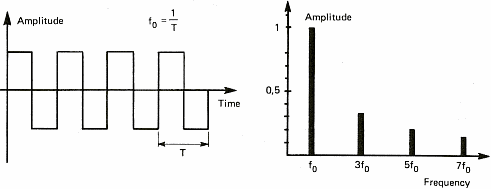
Die Diagramme in Abbildung 6 zeigen ein paar Tonsignale. Wir verwenden diese Diagramme, um den Begriff des Spektrums zu veranschaulichen. Das Spektrum eines Signals zeigt die unterschiedlichen Frequenzen, also Tonh�hen, die gemeinsam einen komplexen Klang ausmachen. Wenn wir ein stabiles periodisches Signal betrachten (gleichbleibender Ton), ist das Spektrum �ber die ganze Zeitspanne stabil und zeigt nur einen Wert (ein einzelner Strich in Abbildung 6a rechts). Man kann jeden Klang als eine Zusammensetzung mehrerer T�ne, also Sinuswellen, sehen. Wir werden sp�ter sehen, dass dieses "Aufsplitten" eines periodischen Signals in lauter Sinuswellen zum ersten Mal im 19. Jahrhundert von einem franz�sischen Mathematiker namens Fourier gezeigt worden ist. Diese Erkenntnis wird uns auch erlauben, auf Akkorde einzugehen. In der Zwischenzeit m�chte ich aber bei Sinuswellen bleiben, weil die viel einfacher zu zeichnen sind, als Solos von Jimmy Hendrix...
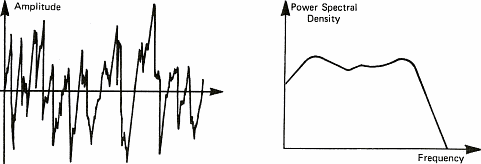
Um Schall mit einem Computer verarbeiten zu k�nnen, m�ssen wir ihn aufnehmen, d.h. wir verwandeln die Ver�nderungen des Luftdrucks in eine Reihe von Zahlen, die der Computer dann versteht. Man verwendet dazu ein Mikrophon, das Luftdruck�nderungen in ein elektrisches Signal verwandelt. Dieses Signal wird dann regelm��ig abgetastet (gesampelt) und der momentane Wert des Signals als Zahl gespeichert. Sampler ist ein allgemeinerer Begriff, und von Elektronikern wird oft der Begriff ADC (Analog to Digital Converter) verwendet. Sampling finden wir auch bei der Soundkarte des PCs. Die Geschwindigkeit, mit der die Soundkarte das Eingangssignal pro Sekunde abtastet und als Zahlen abspeichert (=digitalisiert), wird Abtastfrequenz genannt. Abbildung 7 zeigt den Einfluss der Abtastfrequenz auf ein Signal und sein Spektrum, das mit Hilfe der Fouriertransformation berechnet wurde. F�r die Mathe-Junkies unter uns gibts hier ein paar Formeln:
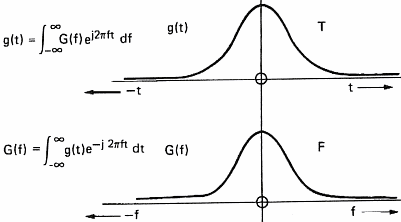

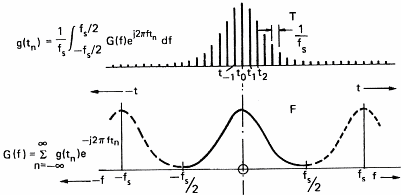
Das zeigt uns (bitte glaub mir), dass die Transformation einer
kontinuierlichen Welle in eine Reihe diskreter Werte das
Spektrum periodisch macht. Ist das Signal ebenfalls periodisch,
dann wird das Spektrum ebenfalls diskret (eine Anzahl von Werten)
und wir brauchen nur mehr mit einer endlichen Anzahl von
Frequenzen zu rechnen. Das sind gute Neuigkeiten, weil unser
Computer nur mit Zahlen und Werten rechnen kann, und nicht mit
Wellen.
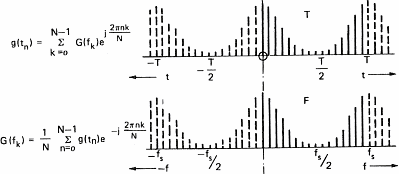
Im Fall der Abbildung 7d ist das Signal sowohl im Zeit- als auch
im Frequenzbereich diskret, im Zeitbereich periodisch und im
Frequenzbereich nur zwischen 0 Hz und der halben Abtastfrequenz.
Mit dem �bergang vom kontinuierlichen zum diskreten Signal
gehen letztendlich Teile des urspr�nglichen
Klangsignals verloren. Der Computer kennt das Klangsignal nur
zu den Abtastzeitpunkten. Um sicherzugehen, dass keine gro�en Verf�lschungen
auftreten, m�ssen wir beim Abtasten ein paar Dinge ber�cksichtigen.
Zum ersten m�ssen wir sicherstellen, dass das Klangsignal keine
Frequenzen enth�lt, die h�her als die halbe Abtastfrequenz sind.
Wenn man das vergisst, werden diese h�heren Frequenzen als
tiefere interpretiert, und das klingt nicht sch�n. Abbildung 8
verdeutlicht uns das:

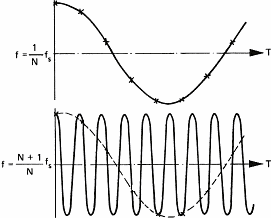
Dieses spezielle Verhalten von abgetasteten Signalen ist als das Shannon'sche Abtasttheorem bekannt, benannt nach dem Mathematiker, der dieses Ph�nomen als erster beschrieben hat. Ein �hnlicher Effekt kann in Filmen, etwa Western, beobachtet werden. Dabei scheinen sich Wagenr�der oft r�ckw�rts zu drehen, was am Stroboskop-Effekt von Filmen liegt. F�r die praktische Anwendung des Musik-Digitalisierens hei�t das, dass man alle Frequenzen oberhalb der halben Abtastfrequenz loswerden muss. Tut man das nicht, wird der Originalton stark verf�lscht. Wenn man z.B. die Abtastfrequenz der Compact Disc betrachtet (44.1 KHz), darf es keine Frequenzen oberhalb von 22 kHz geben. (Sag den Flederm�usen im Haus, sie sollen ruhig sein, die reden n�mlich mit Ultraschall...).
Um die ungewollten Frequenzen loszuwerden, verwendet man Filter. Filter ist ein weitverbreiteter Begriff, der f�r alles verwendet wird, was bestimmte Klangkomponenten herausheben oder umwandeln kann. So verwendet man etwa einen Tiefpassfilter, um hohe Frequenzen zu unterdr�cken, die wir zwar nicht h�ren k�nnen, die aber beim Abtasten l�stig sind (das Traschen der Flederm�use also). Ohne jetzt n�her darauf einzugehen, zeigt das folgende Diagramm die Eigenschaften eines Filters:
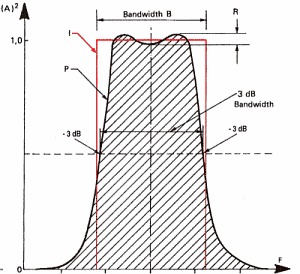
Ein Filter ver�ndert das Signal sowohl im Zeit- als auch
im Frequenzbereich. Eine 100 Hz Rechteckwelle, in der Frequenzen
ab 200 Hz weggefiltert werden, wird zur Sinuswelle, weil der obere
Teil des Spektrums entfernt wurde (siehe Abbildung 6c). �hnlich
wird ein Klavierton von 1000 Hz, der bei 1200 oder 1500 Hz gefiltert
wird, ganz anders klingen. Die niedrigste Frequenz eines Signals wird
Grundfrequenz genannt, die anderen sind Vielfache davon und werden
harmonische Frequenzen genannt.
Im Zeitbereich verursacht ein Filter Ver�nderungen der Welle, die
man Verzerrungen nennt. Das wird haupts�chlich durch die Verz�gerung jeder Harmonie relativ zu den anderen,
verursacht.
Um den Einfluss eines Filters auf ein Signal zu zeigen, betrachten wir einmal einen einfachen Rechteckimpuls (Abbildung 10a), die Amplitude seines Spektrums im Frequenzbereich (Abbildung 10b) und die Phase seines Spektrums (Abbildung 10c). Dieser Rechteckimpuls arbeitet wie ein Filter, der nur Signale zwischen t=0 and T Sekunden durchl�sst. Das Spektrum des Impulses stellt die Frequenzantwort des Filters dar. Wir sehen, dass eine h�here Frequenz des Signals zu einer gr��eren Verz�gerung zwischen den Frequenzkomponenten f�hrt, und zu einer niedrigeren Amplitude.
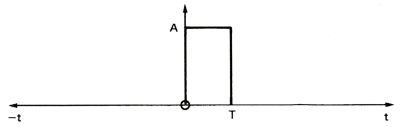

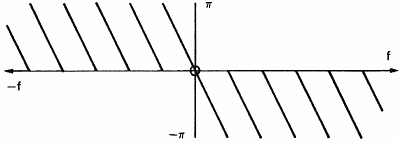
Abbildung 11 zeigt den Einfluss des Rechteckfilters auf ein einfaches Signal wie eine Sinuswelle
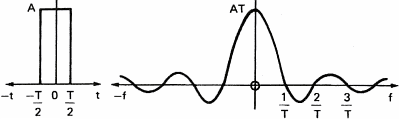
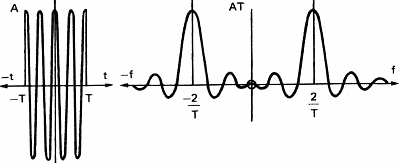
Wenn man den Klang abrupt beim Zeitpunkt T abschneidet, f�hrt das zur Bildung neuer Frequenzen im Spektrum der Sinuswelle. Wenn das gefilterte Signal komplexer ist, wie etwa die Rechteckwelle von Abbildung 6c, werden Frequenzkomponenten zur�ckbleiben und zu einem verzerrten Signal am Ausgang des Filters f�hren.
Um ein besseres Verst�ndnis von Akustik und Schall zu bekommen, besch�ftigen
wir uns doch mal mit dem Teil, den wir dabei am meisten brauchen, dem Ohr.
Abbildung 12 zeigt einen Querschnitt des Ohrs. Schall wird in der Ohrmuschel
aufgefangen und gelangt durch den H�rkanal zum Trommelfell, das mehr oder weniger
wie ein Mikrofon arbeitet. Die Vibrationen des Trommelfells werden von drei
kleinen Kn�chelchen, die wie Hebel wirken, verst�rkt. Sie hei�en Hammer,
Amboss und Steigb�gel.
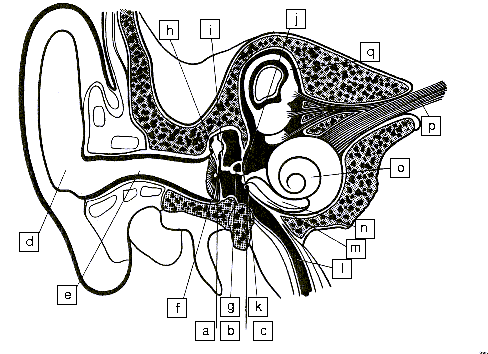 |
a) �u�eres Ohr b) Mittelohr c) Inneres Ohr d) Ohrmuschel e) H�rkanal f) Trommelfell g) Steigb�gel h) Malleus i) Amboss j) Oval Window k) Round Window l) Ohrtrompete m) Paukentreppe n) Scala vestibuli o) Schnecke p) Geh�r- und Gleichgewichtsnerv q) Bogeng�nge des Gleichgewichtsorgans |
|
| Abbildung 12: Die wichtigsten Teile des Ohrs | ||
Die Bewegungen des Steigb�gel-Knochens werden �ber das Oval Window zur Ohrschnecke �bertragen. Die Schnecke enth�lt zwei Kammern, getrennt durch die Basilarmembran, die mit empfindlichen Haaren bedeckt ist und mit dem H�rnerv verbunden ist (wie Abbildung 13 und 14 unten zeigen). Die Basilarmembran hilft bei der Wahrnehmung des Schalls, weil die unterschiedlichen Teile der H�rschnecke auf verschiedene Frequenzen mehr oder weniger empfindlich sind. Das erlaubt dem Gehirn, die Tonh�he von Noten zu unterscheiden.
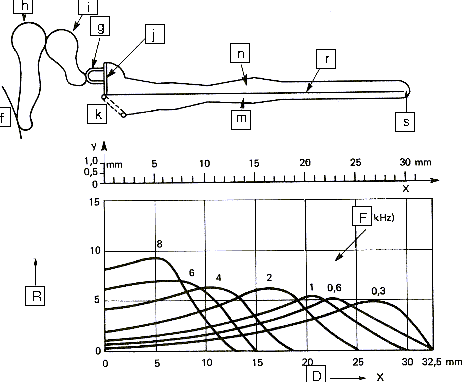 |
f) Trommelfell g) Steigb�gel h) Hammer i) Amboss j) Oval Window k) Round Window m) Paukentreppe n) Scala Vestibuli r) Basilarmembran s) Helicotrema R) Relative Antwort F) Frequenzantwort D) Distance along membrane |
|
| Abbildung 13: L�ngsschnitt der H�rschnecke | ||
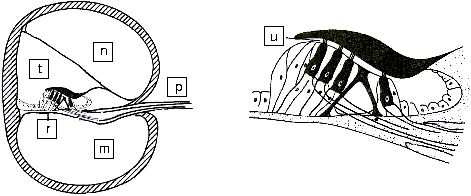 |
m) Paukentreppe n) Scala vestibuli p) H�rnerv r) Basilarmembran t) Scala media u) Haarzelle |
|
| Abbildung 14: Querschnitt der H�rschnecke | ||
Das Gehirn spielt eine sehr wichtige Rolle, weil es f�r die gesamte
Auswertung des Schalls sorgt. Es macht es m�glich, dass wir Ger�usche
und Kl�nge erkennen, je nach Tonh�he und Dauer. Das Gehirn erm�glicht
auch r�umliches H�ren, indem es die Signale beider Ohren vergleicht.
Es erm�glicht uns, Musikinstrumente oder Menschen zu erkennen, und
ihre r�umliche Position festzustellen. Es scheint, dass die meiste
Arbeit, die das Gehirn leistet, angelernt wurde.
Abbildung 15 zeigt, wie wir Schall abh�ngig von der Frequenz h�ren.
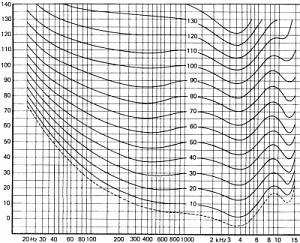
Diese Kurven wurden f�r die Durchschnittsbev�lkerung ermittelt, sind ein statistischer Mittelwert f�r Menschen zwischen 18 und 25 Jahren und gelten f�r reine T�ne. Unterschiede zwischen Personen k�nnen durch viele Faktoren erkl�rt werden, z.B.:
Abbildung 16 zeigt den Einfluss des Alters auf die F�higkeit, hohe Frequenzen wahrzunehmen. Auf die Quellen bezogen sind die Ergebnisse recht unterschiedlich. Das kann leicht erkl�rt werden durch gro�e Unterschiede in der Bev�lkerung und weil solche Studien nicht einfach nur das Alter in Betracht ziehen. Nicht selten findet man schon etwas �ltere Musiker mit "junggebliebenen" Ohren, genauso wie es junge Menschen mit betr�chtlichen Geh�rsch�den gibt. Gr�nde f�r fr�he H�rsch�den sind dabei oft zu lange Konfrontation mit Schall in extremer Lautst�rke, etwa in Konzerten oder Diskotheken.
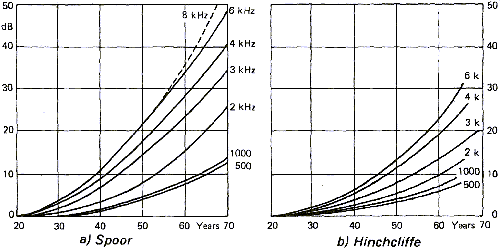
Ob extreme Schalleinwirkung das Geh�r dauerhaft verschlechtert, h�ngt
sowohl von der Dauer als auch von der Lautst�rke ab. Wichtig ist,
dass jede Form von Schall sch�dlich sein kann. Laute Musik mit
dem Kopfh�rer hat dieselben Auswirkungen auf die H�rzellen wie
der Rasenm�her oder ein startendes Flugzeug.
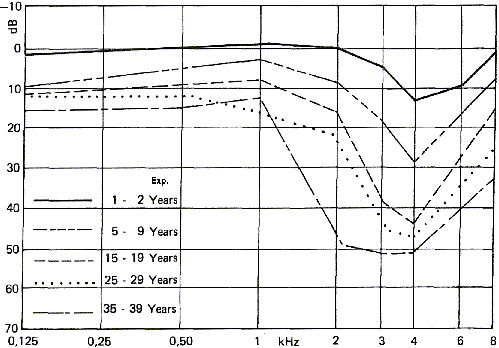
Abbildung 17 zeigt die Auswirkung von extremer Schalleinwirkung
auf das Geh�r. Beachte, dass dieser Effekt nicht derselbe ist wie
der durch das Altern verursachte Geh�rverlust. Dabei kann das
Ohr hohe Frequenzen schlechter wahrnehmen. Extreme Schalleinwirkung
aber vermindert das H�rverm�gen f�r Frequenzen von 3-4 KHz. Bei diesen
Frequenzen ist das gesunde Ohr am empfindlichsten. Diese Art
von Geh�rsch�digung findet man oft bei Benutzern von Schusswaffen.
Wenn wir Blick auf das Kapitel �ber Dezibel (und wie man�s berechnet),
werfen, sehen wir, dass schon zehn Dezibel einen sehr gro�en
Unterschied im Schalldruck ausmachen. Die lineare Dezibelskala
entspricht n�mlich einer exponentiellen Skala des Schalldrucks.
Grund daf�r ist, dass Ohr und Gehirn Schall von sehr unterschiedlicher
Amplitude und Frequenz verarbeiten k�nnen. Die h�chste Frequenz, die
der gesunde Mensch h�ren kann, ist 1000 Mal h�her als die niedrigste,
und der lauteste Ton hat einen eine Million Mal h�heren Schalldruck
als der leiseste Ton, den wir zu h�ren imstande sind
(ein Intensit�tsverh�ltnis von 1012
to 1).
Den Schalldruck zu verdoppeln entspricht gerade mal 3 dB. Das kann man
zwar h�ren, aber es braucht 9 dB, um dem Menschen den subjektiven Eindruck von
doppelter Lautst�rke zu vermitteln. Dabei ist aber der Schalldruck
8 Mal h�her!
Im Frequenzbereich entspricht ein Wechsel der Oktave dem Verdoppeln
der Frequenz. Auch hier h�ren wir den eigentlich exponentiellen
Anstieg der Frequenz auf lineare Art und Weise - ein physikalisches
Ph�nomen. Greif noch nicht zum Taschenrechner, die Tonh�hen der Noten
werden wir sp�ter berechnen.
Aufnahmen mit einem analogen Ger�t wie einem Kassettenrecorder sind nach wie vor gebr�uchlich, auch wenn sie langsam von digitalen Systemen verdr�ngt werden. In beiden F�llen f�hrt die Umsetzung der Schallwelle in magnetische Schwingungen oder digitale Daten zu Ver�nderungen des Signals, was an den Grenzen des aufnehmenden Ger�tes liegt. Wir haben schon kurz dar�ber gesprochen, wie sich das Abtasten eines Signals auf sein Spektrum auswirkt. �hnliche Effekte sieht man, wenn man ein Signal aufnimmt:
"Dynamik" bezeichnet die Differenz zwischen der kleinsten
und gr��ten Amplitude, die ein Aufnahmeger�t erfassen kann.
Das beginnt im Allgemeinen mit dem Mikrophon, das Schall in
ein elektrisches Signal konvertiert, und endet mit dem verwendeten
Aufnahmemedium, der CD, der Kassette oder dem Computer...
Erinnern wir uns daran, dass Dezibel ein Verh�ltnis angeben.
Im Dynamikbereich bezeichnet 0 dB also den unteren Grenzwert.
Ein paar Beispiele:
Ein Orchester kann bis zu 110 dB erreichen. Das ist auch der Grund daf�r, dass Aufnahmetechniker Systeme verwenden, die den Dynamikbereich komprimieren k�nnen, sodass Teile mit hoher Lautst�rke nicht abgeschnitten werden und leisere nicht im Hintergrundrauschen verloren gehen.
Aufnahmeger�te sind weniger leistungsf�hig als das menschliche Ohr und haben den zus�tzlichen Nachteil, selbst Ger�usche zu produzieren. Das kann Kratzen des Tonabnehmers an der Vinylschallplatte sein, oder auch ein Summen des Verst�rkers. Diese Ger�usche sind zwar meist sehr leise, aber sie erlauben es uns nicht, leiseste Kl�nge aufzunehmen. Man h�rt es am besten, wenn man Kopfh�rer von guter Qualit�t verwendet und es klingt wie ein Wasserfall, da es ein sehr weites Spektrum mit vielen Frequenzen enth�lt.
Fr�her haben wir gesehen, dass Filter einen wichtigen Effekt
auf die Phase eines Spektrums haben, weil sie Signale je nach
Frequenz verschieben. Diese Art der Signalverzerrung nennt man
harmonische Verzerrung, weil es alle harmonischen Frequenzen
eines Signals betrifft.
Jedes einzelne Aufnahmeger�t verh�lt sich wie ein Filter und
induziert Signalverzerrungen. Nat�rlich passiert dasselbe bei der
Wiedegabe, wo zus�tzliche Verzerrungen und Rauschen dazukommen.
Mehr und mehr verwendet man Komprimierungsalgorithmen wie mp3
oder Ogg Vorbis, um wertvollen Plattenplatz am Aufnahmemedium
zu sparen.
Man sagt, dass diese Algorithmen verlustbehaftet sind,
weil sie Teile des Signals entfernen, um die Dateigr��e zu minimieren.
Komprimierungsalgorithmen benutzen ein Computermodell des menschlichen
Ohrs, um unh�rbare Information zu l�schen. Zum Beispiel kann man
im Frequenzbereich bei zwei eng benachbarten Frequenzen, die in der
Lautst�rke sehr unterschiedlich sind, die leisere Frequenz l�schen,
weil sie von der lauten �bert�nt wird.
H�rtests und Ratschl�ge, wie man solche Software verwendet, um den
besten Teil des Signals zu erhalten, findet man im Internet.
Soweit der Autor informiert ist, verwendet mp3
einen Tiefpass-Filter, der Frequenzen gr��er 16 KHhz wegfiltert,
und sie erlauben keine Bitraten gr��er als 128 KiloBits/Sekunde.
Mit diesen Zahlen l�sst sich meist keine CD Qualit�t erreichen.
Komprimierungsverfahren wie gzip, bzip2, lha oder zip ver�ndern
hingegen keine Daten, erreichen aber daf�r keine so hohen
Kompressionsraten. Ausserdem ist es n�tig, die ganze Datei zu
entpacken, bevor man sie h�ren kann, was man bei einem Walkman
oder einem handels�blichen Abspielger�t wohl kaum gebrauchen kann.
Um einen Ausgleich zu schaffen, folgt hier ein Vergleich von Begriffen aus der Musik und der Technik. Meist hinken diese Vergleiche, denn die Begriffe, die Musikliebhaber verwenden, beschreiben menschliche Eindr�cke und nicht physische Ph�nomene.
Eine Note ist u.a. durch seine Tonh�he definiert, und diese Tonh�he ist gleichzeitig die Grundfrequenz der Note. Wenn man das wei�, kann man die Frequenzen einer Note mit der folgenden Formel berechnen:
Wenn wir f�r REF A mit 440 Hz von der Oktave 4 als Basis einsetzen, k�nnen wir die anderen Frequenzen f�r T�ne von 1 bis 12 von C bis B berechnen:
| Note | Oktave | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| C | 32,70 | 65,41 | 130,8 | 261,6 | 523,3 | 1047 | 2093 | 4186 |
| C # | 34,65 | 69,30 | 138,6 | 277,2 | 554,4 | 1109 | 2217 | 4435 |
| D | 36,71 | 73,42 | 146,8 | 293,7 | 587,3 | 1175 | 2349 | 4699 |
| E b | 38,89 | 77,78 | 155,6 | 311,1 | 622,3 | 1245 | 2489 | 4978 |
| E | 41,20 | 82,41 | 164,8 | 329,6 | 659,3 | 1319 | 2637 | 5274 |
| F | 43,65 | 87,31 | 174,6 | 349,2 | 698,5 | 1397 | 2794 | 5588 |
| F # | 46,25 | 92,50 | 185,0 | 370,0 | 740,0 | 1480 | 2960 | 5920 |
| G | 49,00 | 98,00 | 196,0 | 392,0 | 784,0 | 1568 | 3136 | 6272 |
| A b | 51,91 | 103,8 | 207,6 | 415,3 | 830,6 | 1661 | 3322 | 6645 |
| A | 55,00 | 110,0 | 220,0 | 440,0 | 880,0 | 1760 | 3520 | 7040 |
| B b | 58,27 | 116,5 | 233,1 | 466,2 | 932,3 | 1865 | 3729 | 7459 |
| B | 61,74 | 123,5 | 246,9 | 493,9 | 987,8 | 1976 | 3951 | 7902 |
Der wahre Musikliebhaber wird bemerken, dass wir nicht
zwischen diatonischen und chromatischen Halbt�nen unterscheiden.
Mit minimalen �nderungen kann man dieselben Berechnungen mit
Kommas als Unterteilung anstatt von Halbt�nen durchf�hren...
Um zu unterscheiden, mit welchem Instrument ein Ton gespielt
wurde, reicht es nicht, nur davon auszugehen, dass jeder Ton aus
verschiedenen Frequenzen besteht... Man muss auch in Betracht
ziehen, wie der Ton gespielt wird (pizzicato oder legato), von
welchem Instrument es kommt, ganz abgesehen von alle m�glichen
Effekten wie glissando, vibrato, etc... F�r diesen Zweck kann
man das Sonogramm eines Tons untersuchen, d.h. Ver�nderungen
des Spektrums durch die Zeit. Ein Sonogramm erlaubt es, alle
harmonischen Frequenzen �ber die Zeitachse zu sehen.

| Abbildung 18: Ein Sonogramm | ||
| T: Zeit | A: Amplitude | F: Frequenz |
Heutzutage verwendet man bei elektronischer Tonaufnahme
und Wiedergabe g�nzlich k�nstliche Ger�te wie Synthesizer,
um Kl�nge praktisch aus dem Nichts zu erzeugen, oder Sampler,
um Kl�nge abzuspeichern und bei verschiedenen Tonh�hen mit
diversen Effekten wiederzugeben. Es ist dann etwa m�glich,
ein Cellokonzert so zu spielen, dass man die Originalinstrumente
durch gesampelte "knarrende St�hle" ersetzt. Und das kann
wirklich jeder tun, man muss kein Instrument spielen k�nnen.
Die Merkmale einer einzelnen Note sind im folgenden Diagramm
gegeben:
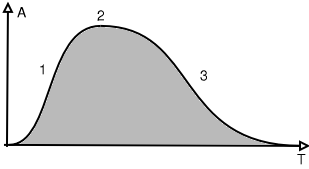
| Abbildung 19: Merkmale einer Note: H�llkurve | |
| 1: Attack | A: Positive Amplitude |
| 2: Sustain | T: Zeit |
| 3: D�mpfung | |
Diese Kurve zeigt die Entwicklung der Gesamtlautst�rke eines Tons
�ber die Zeit. Diese Art Kurve nennt man H�llkurve, weil es das Signal
(grauer Teil des Signals) einh�llt. Der ansteigende Teil wird "attack"
genannt und kann je nach Instrumenttyp stark variieren. Den zweiten Teil
nennt man "sustain", das ist der K�rper des Tons und oft der l�ngste Teil,
abgesehen bei Percussion Instrumenten. Der dritte Teil kann auch je nach
Instrument in Form und L�nge variabel sein.
Zudem erlauben Instrumente Musikern, jeden der drei Bereiche zu beeinflussen.
Unterschiedlicher Anschlag der Klaviertasten wird den attack-Bereich des
Tons beeinflussen, w�hrend die Pedale die D�mpfung ver�ndern werden.
Jeder der drei Bereiche kann sein individuelles Spektrum haben (Farbe),
die die M�glichkeiten an Klangfarben ins Unendliche steigern.
Harmonische Frequenzen �ndern sich nicht im selben Verh�ltnis. Basst�ne
tendieren dazu, l�nger zu dauern, sodass der Klang am Anfang und am
Schluss des Tons nicht derselbe ist.
Gem�� seiner Definition kann der Frequenzbereich eines Ger�ts dem Bereich eines Instruments entsprechen. In beiden F�llen beschreibt der Begriff einen Bereich von Frequenzen oder Tonh�hen, den ein Instrument spielen kann. Wie auch immer, der h�chste Ton, den ein Instrument spielen kann, entspricht der Grundfrequenz in der obigen Tabelle. Anders gesagt, erfordert das Aufnehmen eines Instruments ein Aufnahmeger�t, das einen viel h�heren Frequenzbereich hat als die h�chste Note, die das Instrument spielen kann - sofern man die Klangfarben mit aufnehmen will. Ein schmaler Frequenzbereich wird all die oberen Frequenzen wie ein Tiefpassfilter wegschneiden und die Klangf�lle �ndern. In der Praxis braucht das Aufnahmeger�t einen Frequenzbereich, der dem des menschlichen Geh�rs entspricht, in etwa 20 Hz bis 20 KHz. Oft muss man auch h�her als 20 KHz gehen, weil an der oberen Grenze des Frequenzbereichs oft Verzerrungen auftreten.
Wenn man die obige Tabelle mit den Frequenzen betrachtet, wird
man (als Musiker) �hnlichkeiten zwischen harmonischen Frequenzen
finden und den Noten, die einen Akkord bilden.
Harmonische Frequenzen sind Vielfache der Grundfrequenz.
So sind etwa f�r ein C 1 bei 32.7 Hz die harmonischen Frequenzen folgende:
| Harmonie | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Frequenz | 32,7 | 65,4 | 98,1 | 130,8 | 163.5 | 196,2 | 228,9 | 261,6 |
| Note | C | C | G | C | E | G | B b | C |
Hier sehen wir, warum wir einen Akkord als Tonika (C-E-G-C) oder als Septakkord kennen (C-E-G-Bb): Die Frequenzen der beteiligten Noten schwingen im Einklang mit den harmonischen Frequenzen des Grundtons (C). Darin liegt die Magie.
Ohne zuviel ins Detail zu gehen, haben wir physikalische, biologische und technische Aspekte von Schall und Akustik betrachtet. Unser Ohr ist immer das beste Auswahlkriterium, und wird es auch immer sein. Zahlen, die uns Mathematiker liefern, oder hochentwickelte Messger�te k�nnen uns zwar verstehen helfen, warum eine bestimmte Aufnahme so klingt wie sie klingt. Aber sie werden uns nie sagen k�nnen, ob in den 60ern die Beatles oder die Rolling Stones die bessere Musik gemacht haben.
Br�el & Kjaer: D�nische Firma, die Messger�te f�r Akustik und Schwingungen herstellt. Dieses Unternehmen publiziert seit langer Zeit (50 Jahreungef�hr) frei verf�gbare B�cher, aus denen die meisten in diesem Artikel verwendeten Abbildungen stammen. Die B�cher sind im PDF Format frei verf�gbar unter http://www.bksv.com/bksv/2148.htm