Eine Einf�hrung in die Kryptographie

ArticleCategory:

System Administration

AuthorImage:

TranslationInfo:[Author and translation history]

original in fr Pierre Loidreau

fr to en Axelle Apvrille

en to de Guido Socher

AboutTheAuthor

Pierre arbeitet als Wissenschaftler und Lehrer bei der ENSTA (Ecole Nationale Supérieure de Techniques Avancées). Er arbeitet auf dem Gebiet Kryptosysteme und Fehlerkorrekturcodes. Er "spielt" fast jeden Tag mit Linux herum und manchmal spielt er Tennis.

Abstract:

Dieser Artikel wurde zuerst in der "Security Spezialausgabe" des Linux Magazine France ver�ffentlicht. Der Editor, die Autoren und die �bersetzer haben freundlicherweise LinuxFocus die Erlaubnis gegeben, alle Artikel dieser Spezialausgabe zu ver�ffentlichen, sobald diese auf Englisch verf�gbar sind. Ein gro�es Dankesch�n geht an alle, die bei dieser Arbeit beteiligt sind. Dieser Absatz wird in jedem Artikel dieser Serie erscheinen.

ArticleIllustration:

ArticleBody:[The article body]

Warum Kryptographie -- 2500 Jahre Geschichte

Die Geschichte der Kryptographie geht zur�ck zu den Urspr�ngen der Menschheit, als Menschen anfingen miteinander zu kommunizieren. Sie hatten das Bestreben auch geheime Nachrichten auszutauschen, auf eine sichere Art. Die erste gezielte Anwendung von technischen Methoden um Nachrichten zu verschl�sseln geht auf die Griechen zur�ck. Sie benutzten um 6 vor Christus einen Stock namens "scytale". Der Sender einer Nachricht w�rde ein Papier um diesen Stock rollen und seine Nachricht der L�nge nach darauf schreiben. Danach w�rde er das Papier wieder vom Stock abrollen und verschicken. Der Empf�nger w�re nicht in der Lage die Nachricht zu lesen, ohne die genaue Dicke des Stocks zu kennen. Die Stockdicke war also der geheime Schl�ssel. Sp�ter haben r�mische Heere Caesar's Code benutzt, um Botschaften auszutauschen. Caesar's Code verschiebt das Alphabet um drei Buchstaben.

In den n�chsten 19 Jahrhunderten wurden mehr oder weniger clevere experimentelle Verschl�sselungsverfahren entwickelt. Ihre Sicherheit hing davon ab, wieviel Vertrauen der Benutzer in dieses Verfahren hatte. Im 19. Jahrhundert schrieb Kerchoff eine der Prinzipien der modernen Kryptographie. Es besagt, da� die Sicherheit eines kryptographischen Systems nicht in dem Verfahren der Verschl�sselung liegt, sondern von der L�nge des verwendeten Schl�ssels abh�ngt.

Von diesem Augenblick an konnte man erwarten, da� kryptographische Systeme dieser Anforderung gerecht wurden. Es fehlte jedoch noch an mathematischem Hintergrund und Werkzeugen, um die Widerstandsf�higkeit gegen Angriffe zu testen. 1948 und 1949 untermauerte Claude Shannon die moderne Kryptographie mit zwei Ver�ffentlichungen: "A Mathematical Theory of Communication" und "The Communication Theory of Secrecy Systems". Diese zwei Artikel fegten Hoffnungen und Vorurteile gleicherma�en hinweg. Shannon best�tigte, da� Vernam's Cipher, die einige Jahre zuvor vorgeschlagen worden war, auch als One Time Pad (einmal Schl�ssel) bekannt, das einzige sichere System war, das es jemals geben kann. Leider war dieses System in der Praxis unbenutzbar.... Das ist der Grund, warum die Sicherheit eines Systems heute an dem Rechenaufwand zum Entschl�sseln gemessen wird. Man behauptet, da� ein System sicher ist, wenn kein bekannter Angriff einfacher ist als das Durchprobieren aller m�glichen Schl�ssel.

AES (Advanced Encryption Standard)

K�rzlich, im Oktober 2000, hat das NIST (National Institute of Standards and Technology) einen neuen Standard zur Verschl�sselung unter 15 Kandidaten ausgew�hlt. Dieser neue Standard soll den alten DES Algorithmus abl�sen. Rijndael -- ein Phantasiename aus den Namen der Erfinder, Rijmen und Daemen, wurde als AES ausgew�hlt.

Dieses kryptographische System wird als "block cipher" bezeichnet, da es 128-Bit Bl�cke verschl�sselt. Verschiedene Optionen erlauben die Benutzung von Schl�sseln der L�nge 128, 192 oder 256 Bit. Nur zu deiner Information: Der DES war eine 64 Bit "block cipher" mit einer Sch�ssell�nge von 56 Bit. Tripple-DES verschl�sselt 64 Bit Bl�cke mit einer Sch�ssell�nge von 112-Bit.

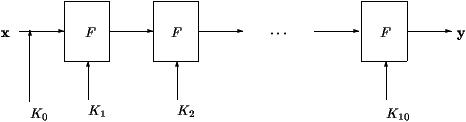
Abb. 1: AES Iterationen
Das Verfahren von AES ist in Abb. 1 beschrieben. Zun�chst wird der geheime Schl�ssel K0 mit der Nachricht ver-XOR-ed. Danach wir die Funktion F iterativ (wie bei allen "block ciphers") angewandt, unter Benutzung von Unterschl�sseln, die durch eine Sch�sselexpansionsroutine erzeugt werden.

F�r AES wird die Funktion F 10 mal angewandt.

Abbildung 2 beschreibt wie die Funktion F zum Verschl�sseln iteriert wird. Ein 128-Bit Block wird in 16 Bytes unterteilt. Zuerst wird die Substitution S auf jedes Byte angewendet. Danach wird die Permutation P auf die 16 Bytes angewandt. Der 128-Bit Teilsch�ssel aus der Schl�sselexpansionsroutine wird dann Bitweise hinzuaddiert.
Der Schl�ssel Ki von Runde n°i ergibt sich aus der Schl�sselexpansion von Unterschl�ssel K(i-1) aus Runde n°i-1 und K0 ist der geheime Schl�ssel. Die Sch�sselexpansionsroutine ist in Abbildung 3 beschrieben. Die 16 Bytes von Schl�ssel K(i-1) werden in Viererbl�cken bearbeitet.
Die letzten vier Bytes werden mit der Substitution S - dieselbe Substitution, die in Funktion F benutzt wird - bearbeitet. Danach werden die 4 resultierenden Bytes zu dem Alpha-Element hinzugef�gt. Dieses Element ist ein vordefiniertes Element, das von der Nummer der Iteration abh�ngt. Um letztlich Ki zu erhalten, werden die resultierenden 4 Bytes bitweise zu den ersten 4 Bytes von K(i-1) addiert. Danach wird das Ergebnis zu den n�chsten 4 Bytes hinzugef�gt u.s.w...

Abb 2: Funktion F
Nun wollen wir noch schnell sehen, wie die Substitutionen gebaut werden und wof�r die Konstanten aⁱ gebraucht werden. Technisch und aus Gr�nden der einfachen Berechnung, wird ein Byte als ein Element aus einer Menge von 256 Elementen betrachtet, genannt Finite Field. In einem Finite Field existieren einfache Operationen wie Addition, Multiplikation und Inverses-Element. Die Substitution S ist die Inverse eines solchen Finite Field.
Die Substitution S ist eine sehr einfache Operation und kann deshalb leicht implementiert werden. Element aⁱ ist einfach die i-te Potenz im Finite Field. Das macht die AES sehr effizient.

Da AES nur mit einfachen Bit Operationen arbeitet hat es zwei Vorteile:

Selbst reine Softwareimplementationen von AES sind schnell. Z.B bietet eine C++ Implementation auf einem Pentium 200Mhz eine Geschwindigkeit von 70Mbits/s.
AES is resistent gegen lineare und differentielle Kryptoanalyse, da AES nicht wie DES von der Wahl der S-Box abh�ngt, von der immer vermutet wurde, da� sie eine Hintert�r f�r den NSA war.

Abb. 3: Schl�sselexpansion

Public Key Cryptography

Im Jahr 1976 haben Diffie und Hellman einen Artikel mit dem Titel "New Directions in Cryptography" ver�ffentlicht, der zum Renner in der Kryptographiegemeinde wurde. Dieser Artikel stellte ein neues Konzept vor: Public Key Cryptography. Die bis zu dieser Zeit bekannten symmetrischen Algorithmen mit geheimen Schl�ssel wurden nicht mehr den Bed�rfnissen der modernen Kommunikation gerecht.

Das neue an Public Key Cryptography war die Idee der Trapdoor One-Way Functions. Diese Funktionen lassen sich einfach in einer Richtung berechnen, aber es gibt keine gute M�glichkeit, die Umkehrfunktion zu berechnen. Jedoch haben sie eine Hintert�r und wenn man diese Hintert�r kennt, kann man auch die Umkehrfunktion leicht aufstellen. Mit anderen Worten: Alle k�nnen Nachrichten verschl�sseln, aber nur der, der die Hintert�r kennt, kann die Nachricht wieder entschl�sseln. Das war die Geburtsstunde von Alice und Bob. Alice und Bob sind zwei Personen, die geheime Nachrichten austauschen wollen und erfolgreich Eindringlinge schlagen. Eindringlinge, die ihrer Kommunikation lauschen und Daten ver�ndern.

Das sch�nste Beispiel der Public Key Cryptography (und sicher das Einfachste) wurde zwei Jahre sp�ter, 1978, pr�sentiert. Es wurde erfunden von Rivest, Shamir und Adleman und ist daher als RSA bekannt. Es basiert auf der mathematischen Schwierigkeit eine ganze Zahl in Primfaktoren zu zerlegen. Der geheime Schl�ssel besteht aus drei Zahlen (p,q,d) wobei p und q zwei Primzahlen mit ungef�hr gleicher Gr��e sind und d eine relative Primzahl zu p-1 and q-1 und die unten stehende Gleichung erf�llen mu�. Der �ffentliche Schl�ssel besteht aus dem Paar (n,e), wobei n=pq, und e der inverse Modulus von (p-1)(q-1) ist.

ed = 1 mod(p-1)(q-1).

Nehmen wir an, Alice m�chte einen Text verschl�sselt mit Bobs �ffentlichem Schl�ssel verschicken (n,e). Dazu transformiert sie die Nachricht in eine Zahl m kleiner n und dann berechnet sie:

c = m^e mod n,

und schickt c zu Bob. Bob berechnet auf seiner Seite mit dem geheimen Sch�ssel (p,q,d):

c^d mod n = m^ed mod n = m.

Bei RSA ist die Trapdoor One-Way Function die Funktion, die eine ganze Zahl x<n, mit dem Wert x^e mod n assoziiert.

Seit RSA wurden viele andere public key cryptosystems entwickelt. Eine der beliebtesten Alternativen zu RSA ist ein Kryptosystem, das auf diskreten Logarithmen basiert.

Moderne Kryptographie

Public key cryptography ist sehr interessant, weil sie einfach zu benutzen ist und viele Sicherheitsprobleme l�st:

Individuen identifizieren: Wenn Alice mit Bob Nachrichten austauscht, m�chte sie sicher sein, da� es wirklich Bob ist und nicht jemand der vorgibt, Bob zu sein. Dazu benutzt sie ein Identifikationsprotokoll, das im allgemeinen auf RSA oder diskreten Logarithmen basiert.
Dokumentenautentifizierung: Eine autorisierte Stelle autentifiziert ein Dokument mit einer digitalen Signatur. Das Signieren besteht im Anh�ngen von einigen Bits, die aus dem Inhalt des Dokuments und des Schl�ssels der autorisierten Stelle berechnet werden. Das geschieht mit einem Hash Algorithmus wie MD5 oder SHA. Jede Person, die Zugang zu dem Dokument hat, kann �berpr�fen, da� es wirklich von der autorisierten Stelle unterschrieben wurde. Dazu wird ein Signaturschema benutzt. Eines der bekanntesten ist ElGamal -- wieder basierend auf diskreten Logarithmen.

Daneben bietet public key cryptography, genau wie Kryptographie mit geheimen Sch�ssel, eine sichere und geheime Kommunikation.

Nehmen wir an, dass Alice geheim mit Bob kommunizieren m�chte. Alice holt sich dazu aus einem �ffentlichen Verzeichnis den �ffentlichen Sch�ssel von Bob und verschl�sselt damit ihre Nachricht. Bob erh�lt die Nachricht und kann sie mit seinem geheimen Schl�ssel entschl�sseln. Beide Schl�ssel, �ffentlicher Sch�ssel und geheimer Schl�ssel, haben sehr unterschiedliche Rollen. Deshalb nennt man das auch asymmetrische Kryptographie. Bei Systemen mit geheimen Schl�ssel wird derselbe Schl�ssel zum Ver- und Entschl�sseln benutzt (symmetrisch).

Public key cryptography bietet einen weiteren riesigen Vorteil. Wenn n Leute miteinander kommunizieren wollen, dann braucht man bei geheimen Schl�sseln f�r jedes m�glich Paar einen Schl�ssel. Also n(n-1) Schl�ssel. Bei Public key cryptography braucht man nur n Schl�ssel. Ein riesiger Vorteil, wenn mehr als tausend Leute miteinander reden m�chten. Weiterhin ist es schwierig, mit symmetrischer Kryptographie ein neues Mitglied in die Gruppe einzuf�hren. Man m��te dazu n Schl�ssel erzeugen und sie auf einem sicheren Weg an alle verteilen. Im Gegensatz dazu braucht man bei public key cryptography lediglich einen neuen Schl�ssel im Schl�sselverzeichnis zu ver�ffentlichen.

�ffentlicher Schl�ssel oder geheimer Schl�ssel: Die richtige Wahl treffen.

Im vorherigen Abschnitt haben wir gesehen, da� public key cryptography viele Probleme l�st die Kryptographie mit geheimem Schl�ssel nicht l�sen kann. Da mag man sich fragen, warum AES, ein symmetrisches Verfahren (geheimer Schl�ssel), entwickelt wurde. Es gibt zwei wesentliche Gr�nde:

Zun�chst einen praktischen Grund. Public key cryptosystems sind sehr langsam. Eine Software Implementation von AES ist tausend mal schneller als RSA und RSA ist fast unm�glich in Hardware zu implementieren. Eine AES Hardwareimplementation ist m�glich und liefert h�chste �bertragungsgeschwindigkeit.
Die innere Struktur von public key cryptosystems f�hrt zu anderen Sicherheitsproblemen.

Public key cryptosystems brauchen viel l�ngere Schl�ssel im Vergleich zu symmetrischen Verfahren, um gleiche Sicherheit zu gew�hrleisten. Bei einem symmetrischen Verfahren ist die Sicherheit so gut wie der Aufwand, alle m�glichen Schl�sselkombinationen zu testen. Bei einer Schl�ssell�nge von 128 Bit mu� man also 2¹²⁸ Kombinationen testen.

Bei public key cryptosystems ist das nicht so. Ein RSA mit 512 Bit ist weit weniger sicher als AES mit 128 Bit. Die einzige M�glichkeit, die Sicherheit eines public key cryptosystems zu berechnen, ist den Aufwand f�r den momentan besten bekannten Angriff zu berechnen. Eine Gruppe von Forschern hat es k�rzlich geschafft, eine 512 Bit Zahl zu faktorisieren. Der allgemeine Hinweis ist jetzt, da� man 1024 Bit RSA benutzen soll.

Zum reinen Verschl�sseln sind also symmetrische Verfahren besser. Zimmermann hat ein interessantes Verfahren ausgearbeitet, da� sowohl asymmetrische als auch symmetrische Verfahren benutzt: PGP. Wenn Alice und Bob kommunizieren wollen, dann sieht das so aus:

Alice und Bob handeln einen geheimen Schl�ssel mit einem Sch�sselaustauschprotokol aus. Dieses Protokoll benutzt public key cryptography. Z.B mit dem Diffie-Hellman Algorithmus.
Danach kommunizieren sie mit einem symmetrischen Verfahren, z.B mit dem IDEA Algorithmus.

Nach der Kommunikation wird der geheime Schl�ssel (session key) einfach vernichtet. Normalerweise ist der leichter angreifbare Teil der Kommunikation das Schl�sselaustauschprotokoll mit public key cryptography.

Bibliografie

Geschichte der Kryptographie:

S. Singh : Histoire des codes secrets. Jean-Claude Lattès, 1999.
D. Kahn : The Codebreakers: the story of secret writing. MacMillan publishing, 1996.

Zu AES :

Kryptographie im Allgemeinen :

Artikel von Anne Canteaut und Fran Lévy-dit-Véhel : http://www-rocq.inria.fr/canteaut/crypto_moderne.pdf
B. Schneier : Applied Cryptography. John Wiley and Sons, 1996.