Introducci�n
Definici�n. Un �rbol AVL es un �rbol binario de b�squeda que cumple con la condici�n de que la diferencia entre las alturas de los sub�rboles de cada uno de sus nodos es, como mucho 1.
La denominaci�n de �rbol AVL viene dada por los creadores de tal estructura (Adelson-Velskii y Landis).
Recordamos que un �rbol binario de b�squeda es un �rbol binario en el cual cada nodo cumple con que todos los nodos de su sub�rbol izquierdo son menores que la ra�z y todos los nodos del sub�rbol derecho son mayores que la ra�z.
Recordamos tambi�n que el tiempo de las operaciones sobre un �rbol binario de b�squeda son O(log n) promedio, pero el peor caso es O(n), donde n es el n�mero de elementos.
La propiedad de equilibrio que debe cumplir un �rbol para ser AVL asegura que la profundidad del �rbol sea O(log(n)), por lo que las operaciones sobre estas estructuras no deber�n recorrer mucho para hallar el elemento deseado. Como se ver�, el tiempo de ejecuci�n de las operaci�nes sobre estos �rboles es, a lo sumo O(log(n)) en el peor caso, donde n es la cantidad de elementos del �rbol.
Sin embargo, y como era de esperarse, esta misma propiedad de equilibrio de los �rboles AVL implica una dificultad a la hora de insertar o eliminar elementos: estas operaciones pueden no conservar dicha propiedad.
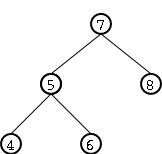
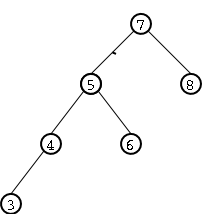
A modo de ejemplificar esta dificultad, supongamos que al �rbol AVL de enteros de Figure 1 le queremos agregar el entero 3. Si lo hacemos con el procedimiento normal de inserci�n de �rbols binarios de b�squeda el resultado ser�a el �rbol de Figure 2 el cual ya no cumple con la condici�n de equilibrio de los �rboles AVL dado que la altura del sub�rbol izquierdo es 3 y la del sub�rbol derecho es 1.
En the Section called Rotaciones simples se pasar� a explicar una serie de operaciones sobre los nodos de un �rbol AVL con las cuales poder restaurar la propiedad de equilibrio de un �rbol AVL luego de agregar o eliminar elementos.