Rotaciones simples

Veremos a continuaci�n una operaci�n sencilla sobre un �rbol binario de b�squeda que conserva el �rden en sus nodos y que nos ayudar� a restaurar la propiedad de equilibrio de un �rbol AVL al efectuar operaciones sobre el mismo que puedan perturbarla.

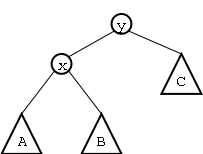
Miremos por un momento el �rbol de Figure 3. Dado que este es un �rbol de b�squeda se debe cumplir x < y y adem�s todos los nodos del sub�rbol A deben ser menores que x y y; todos los nodos del sub�rbol B deben ser mayores que x pero menores que y; y todos los nodos del sub�rbol C deben ser mayores que y y por lo tanto que x.

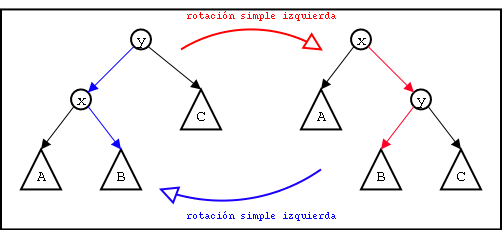
En Figure 4 se ha modificado sencillamante el �rbol. Como puede verificarse f�cilmente por las desigualdades descriptas en el p�rrafo anterior, el nuevo �rbol sigue manteniendo el �rden entre sus nodos, es decir, sigue siendo un �rbol binario de b�squeda. A esta transformaci�n se le denomina rotaci�n simple (o sencilla).

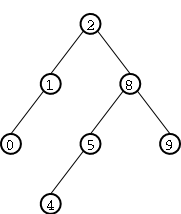
Veamos un ejemplo concreto. Deseamos insertar el n�mero 3 en el �rbol de enteros de Figure 5. La inserci�n se muestra punteada en Figure 6. Sin embargo, como puede verse, la inserci�n a provocado la p�rdida de la propiedad de equilibrio del �rbol ya que dicha propiedad no se cumple en el nodo marcado con rojo. �Qu� hacemos para recomponer dicha pripiedad? Simplemente realizamos una rotaci�n simple. En este caso se dice que la rotaci�n es izquierda ya que la "p�rdida de equilibrio se produce hacia la izquierda. En Figure 7 puede verse el �rbol luego de la rotaci�n: la propiedad de equilibrio ha sido reestablecida. Como mostramos atr�s, la rotaci�n conserva el orden entre los nodos, por lo que podemos afirmar que este �ltimo �rbol si es AVL.

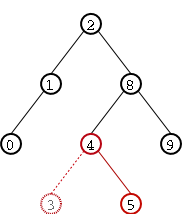
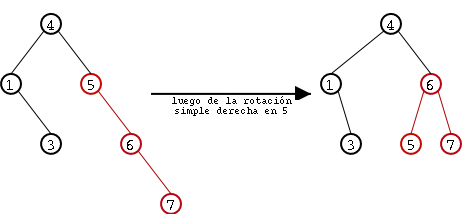
Como podemos observar, el resultado luego de la rotaci�n es un �rbol AVL: posee tanto el �rden correcto de un �rbol de b�squeda entre sus nodos y la propiedad de equilibrio. En este caso el "desequilibrio" en el �rbol con ra�z 5 era enteramente hacia la izquierda y por lo tanto, como ya dijimos, la rotaci�n efectuada se denomina rotaci�n simple izquierda. En el caso de un "desequilibrio" hacia la derecha, la rotaci�n es an�loga y se denomina rotaci�n simple derecha. En Figure 8 se ven dos �rboles: el primero tiene un "desequilibrio hacia la derecha" marcado en rojo y el segundo es el resultado de aplicar una rotaci�n simple derecha.

void rotar_s (AVLTree ** t, bool izq);                     

/* realiza una rotaci�n simple del �rbol t el cual se      
   pasa por referencia. La rotaci�n ser� izquierda
   sii. (izq==true) o ser� derecha
   sii. (izq==false). 

   Nota: las alturas de t y sus sub�rboles ser�n actualizadas
   dentro de esta funci�n!

   Precondici�n:
   si (izq==true) ==> !es_vacio(izquierdo(t)) 
   si (izq==false) ==> !es_vacio(derecho(t))
*/



void
rotar_s (AVLTree ** t, bool izq)                                                      
{
  AVLTree *t1;
  if (izq)	/* rotaci�n izquierda */
    {
      t1 = izquierdo (*t);
      (*t)->izq = derecho (t1);
      t1->der = *t;
    }
  else		/* rotaci�n derecha */
    {
      t1 = derecho (*t);
      (*t)->der = izquierdo (t1);
      t1->izq = *t;
    }

  /* actualizamos las alturas de ambos nodos modificados */
  actualizar_altura (*t);
  actualizar_altura (t1);

  /* asignamos nueva ra�z */
  *t = t1;
}